Patrick Mugisha, "On my honor, as a student, I have neither given nor received unauthorized aid on this academic work."

What statistical techniques are available?

Differences?

Goals

• how to perform t-testing & ANOVA
• t-testing is used to find if there is any statically significant difference in the mean values of two samples
• help to answer many questions such as:
  • any difference in intelligence scores between male and female
  • any difference in cheating on spouse between religous people and people with no religion
  • any difference in profits between small-size models and luxurious hotels

Python packages

• Scipy
• Statsmodels
• pingouin

Install pingouin (a new python package for statistical inference testing)

# install pingouin https://pingouin-stats.org/

!pip install pingouin

#or 

#!pip install pingouin --user

Requirement already satisfied: pingouin in c:\users\patri\appdata\roaming\python\python38\site-packages (0.3.10)
Requirement already satisfied: seaborn>=0.9.0 in c:\users\patri\anaconda3\lib\site-packages (from pingouin) (0.11.0)
Requirement already satisfied: scipy>=1.3 in c:\users\patri\anaconda3\lib\site-packages (from pingouin) (1.5.2)
Requirement already satisfied: numpy>=1.15 in c:\users\patri\anaconda3\lib\site-packages (from pingouin) (1.19.2)
Requirement already satisfied: matplotlib>=3.0.2 in c:\users\patri\anaconda3\lib\site-packages (from pingouin) (3.3.2)
Requirement already satisfied: outdated in c:\users\patri\appdata\roaming\python\python38\site-packages (from pingouin) (0.2.0)
Requirement already satisfied: scikit-learn in c:\users\patri\anaconda3\lib\site-packages (from pingouin) (0.23.2)
Requirement already satisfied: statsmodels>=0.10.0 in c:\users\patri\anaconda3\lib\site-packages (from pingouin) (0.12.0)
Requirement already satisfied: tabulate in c:\users\patri\appdata\roaming\python\python38\site-packages (from pingouin) (0.8.9)
Requirement already satisfied: pandas>=0.24 in c:\users\patri\anaconda3\lib\site-packages (from pingouin) (1.1.3)
Requirement already satisfied: pandas-flavor>=0.1.2 in c:\users\patri\appdata\roaming\python\python38\site-packages (from pingouin) (0.2.0)
Requirement already satisfied: pyparsing!=2.0.4,!=2.1.2,!=2.1.6,>=2.0.3 in c:\users\patri\anaconda3\lib\site-packages (from matplotlib>=3.0.2->pingouin) (2.4.7)
Requirement already satisfied: certifi>=2020.06.20 in c:\users\patri\anaconda3\lib\site-packages (from matplotlib>=3.0.2->pingouin) (2020.6.20)
Requirement already satisfied: cycler>=0.10 in c:\users\patri\anaconda3\lib\site-packages (from matplotlib>=3.0.2->pingouin) (0.10.0)
Requirement already satisfied: pillow>=6.2.0 in c:\users\patri\anaconda3\lib\site-packages (from matplotlib>=3.0.2->pingouin) (8.0.1)
Requirement already satisfied: kiwisolver>=1.0.1 in c:\users\patri\anaconda3\lib\site-packages (from matplotlib>=3.0.2->pingouin) (1.3.0)
Requirement already satisfied: python-dateutil>=2.1 in c:\users\patri\anaconda3\lib\site-packages (from matplotlib>=3.0.2->pingouin) (2.8.1)
Requirement already satisfied: requests in c:\users\patri\anaconda3\lib\site-packages (from outdated->pingouin) (2.24.0)
Requirement already satisfied: littleutils in c:\users\patri\appdata\roaming\python\python38\site-packages (from outdated->pingouin) (0.2.2)
Requirement already satisfied: joblib>=0.11 in c:\users\patri\anaconda3\lib\site-packages (from scikit-learn->pingouin) (0.17.0)
Requirement already satisfied: threadpoolctl>=2.0.0 in c:\users\patri\anaconda3\lib\site-packages (from scikit-learn->pingouin) (2.1.0)
Requirement already satisfied: patsy>=0.5 in c:\users\patri\anaconda3\lib\site-packages (from statsmodels>=0.10.0->pingouin) (0.5.1)
Requirement already satisfied: pytz>=2017.2 in c:\users\patri\anaconda3\lib\site-packages (from pandas>=0.24->pingouin) (2020.1)
Requirement already satisfied: xarray in c:\users\patri\appdata\roaming\python\python38\site-packages (from pandas-flavor>=0.1.2->pingouin) (0.17.0)
Requirement already satisfied: six in c:\users\patri\anaconda3\lib\site-packages (from cycler>=0.10->matplotlib>=3.0.2->pingouin) (1.15.0)
Requirement already satisfied: idna<3,>=2.5 in c:\users\patri\anaconda3\lib\site-packages (from requests->outdated->pingouin) (2.10)
Requirement already satisfied: urllib3!=1.25.0,!=1.25.1,<1.26,>=1.21.1 in c:\users\patri\anaconda3\lib\site-packages (from requests->outdated->pingouin) (1.25.11)
Requirement already satisfied: chardet<4,>=3.0.2 in c:\users\patri\anaconda3\lib\site-packages (from requests->outdated->pingouin) (3.0.4)
Requirement already satisfied: setuptools>=40.4 in c:\users\patri\anaconda3\lib\site-packages (from xarray->pandas-flavor>=0.1.2->pingouin) (50.3.1.post20201107)

import pingouin as pg
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import pandas as pd
from IPython.display import Image

Assumptions of statistical tests

• Many statistical tests assume that the data is normally distributed (parametric data): can be tested using stats.normaltest
• Equal variances between different samples (homogeneity of variance): can be tested using stats.levene

Parametric data looks like this

# looks nornally distributed ... "parametric data"
Image("images/numpy-random-normal.png")

# what does the parametric data look like

np.random.seed(123)   # simulated data
x = np.random.normal(size=50)
plt.hist(x)
#pg.qqplot(x, dist='norm');

(array([ 2.,  1.,  4.,  6., 10.,  7.,  6.,  7.,  3.,  4.]),
 array([-2.79858911, -2.27949367, -1.76039823, -1.24130279, -0.72220736,
        -0.20311192,  0.31598352,  0.83507895,  1.35417439,  1.87326983,
         2.39236527]),
 <BarContainer object of 10 artists>)

pg.qqplot(x, dist='norm');

Non-parametric data looks like this

# looks skewed ... "non-parametric data"
Image(url= "http://www.philender.com/courses/intro/notes3/cheby2.png")

Loading python packages

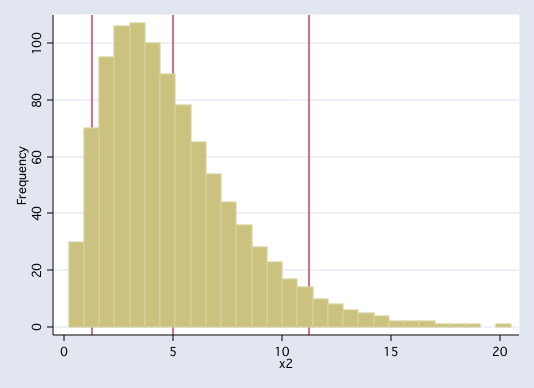
import pandas as pd
import numpy as np
from scipy import stats         
import matplotlib.pyplot as plt
%matplotlib inline

# import the scatter_matrix functionality
from pandas.plotting import scatter_matrix   

import pingouin as pg

import warnings   
warnings.simplefilter(action='ignore', category=FutureWarning) 

import warnings
warnings.filterwarnings("ignore", category=FutureWarning)

Loading data

from pingouin import read_dataset

df = pg.read_dataset('anova')    # this is a toy dataset
df.head()

	Subject	Hair color	Pain threshold
0	1	Light Blond	62
1	2	Light Blond	60
2	3	Light Blond	71
3	4	Light Blond	55
4	5	Light Blond	48

df.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 19 entries, 0 to 18
Data columns (total 3 columns):
 #   Column          Non-Null Count  Dtype 
---  ------          --------------  ----- 
 0   Subject         19 non-null     int64 
 1   Hair color      19 non-null     object
 2   Pain threshold  19 non-null     int64 
dtypes: int64(2), object(1)
memory usage: 584.0+ bytes

df.columns = df.columns.str.replace(' ','')
df.columns = df.columns.str.lower()
df.columns

Index(['subject', 'haircolor', 'painthreshold'], dtype='object')

Exploring data & Data visualization

# basic stats
df.describe()

	subject	painthreshold
count	19.000000	19.000000
mean	10.000000	47.842105
std	5.627314	11.456503
min	1.000000	30.000000
25%	5.500000	40.000000
50%	10.000000	48.000000
75%	14.500000	56.000000
max	19.000000	71.000000

df['haircolor'].value_counts()

Dark Blond        5
Light Blond       5
Dark Brunette     5
Light Brunette    4
Name: haircolor, dtype: int64

# pivot for haircolor
df.groupby('haircolor').mean()

	subject	painthreshold
haircolor
Dark Blond	8.0	51.2
Dark Brunette	17.0	37.4
Light Blond	3.0	59.2
Light Brunette	12.5	42.5

df.boxplot('painthreshold', by='haircolor')

<AxesSubplot:title={'center':'painthreshold'}, xlabel='haircolor'>

Check assumptions

Normality test

# an illustration of normal distribution

h = sorted(df['painthreshold'])
fit = stats.norm.pdf(h, np.mean(h), np.std(h))  #this is a fitting indeed
plt.plot(h,fit,'-o');
plt.hist(h, density=True);      #use this to draw histogram of your data

# test if the data is normally distributed

import scipy.stats as stats

print(stats.normaltest(df['painthreshold']))

NormaltestResult(statistic=0.8897709853074605, pvalue=0.6408976593209752)

C:\Users\patri\anaconda3\lib\site-packages\scipy\stats\stats.py:1603: UserWarning: kurtosistest only valid for n>=20 ... continuing anyway, n=19
  warnings.warn("kurtosistest only valid for n>=20 ... continuing "

# to print three decimals only
pain = stats.normaltest(df['painthreshold'])
print("The chi-square statistic is %.3f and the p-value is %.3f." % pain)

The chi-square statistic is 0.890 and the p-value is 0.641.

p-value is high, it means it is likely that the data is normally distributed.

# using pingouin https://pingouin-stats.org/generated/pingouin.normality.html
pg.normality(df['painthreshold'], method='normaltest').round(3)

	W	pval	normal
painthreshold	0.89	0.641	True

Hypothesis Testing using t-test & ANOVA

t-test

• the most popular statical techique for hypothesis testing
• test if the mean (or average) of two groups or data samples is significantly different or not
• low p-value (< 0.01) is an indicator that there is significant difference in the two groups.

http://www.socialresearchmethods.net/kb/stat_t.php

2-sample test

Our null hypothesis is that ther is no difference between Light Blond and Dark Blond in terms of painthreshold.

df['haircolor'].value_counts()

Dark Blond        5
Light Blond       5
Dark Brunette     5
Light Brunette    4
Name: haircolor, dtype: int64

# comparing two groups

lb = df[df['haircolor'] == 'Light Blond']['painthreshold']
db = df[df['haircolor'] == 'Dark Blond']['painthreshold']

stats.ttest_ind(lb, db)   #using scipy package

Ttest_indResult(statistic=1.4191001323554844, pvalue=0.19363526672361778)

#print three decimal points

two_sample = stats.ttest_ind(lb, db)
print("The t-statistic is %.3f and the p-value is %.3f." % two_sample)

The t-statistic is 1.419 and the p-value is 0.194.

#using pingouin package  https://pingouin-stats.org/generated/pingouin.ttest.html#pingouin.ttest

pg.ttest(lb, db, correction=False).round(2)

	T	dof	tail	p-val	CI95%	cohen-d	BF10	power
T-test	1.42	8	two-sided	0.19	[-5.0, 21.0]	0.9	0.875	0.24

• Null hypothesis says two means are almost same.
• p-value is a probability if the null hypothesis is true. A high p-value (> 0.05) means we can't reject the null hypothesis
• Since we have a high p-value, we accept the null hypothesis that LB and DB are roughly same in terms of painthreshold (No difference)

# test if there is a significant difference in Pain threshhold between the Dark Blond (db) and the Light Brunette (lbr)

lb = df[df['haircolor'] == 'Light Brunette']['painthreshold']
db = df[df['haircolor'] == 'Dark Blond']['painthreshold']

stats.ttest_ind(lb, db)  #using scipy package

#high p-value --> there is no significant difference between lb and db 

Ttest_indResult(statistic=-1.6474689642032443, pvalue=0.14345371872478807)

ANOVA test

• Analaysis of variance (ANOVA) is used to test differences more than three samples or groups

# test any significant differences in tip amounts for thur, fri, sat, and sun
# Anova test

db = df[df['haircolor'] == 'Dark Blond']['painthreshold']
dbr = df[df['haircolor'] == 'Dark Brunette']['painthreshold']
lb = df[df['haircolor'] == 'Light Blond']['painthreshold']
lbr = df[df['haircolor'] == 'Light Brunette']['painthreshold']

f_val, p_val = stats.f_oneway(db, dbr, lb, lbr)  
  
print("One-way ANOVA P =", p_val)

One-way ANOVA P = 0.00411422733307741

painthreshold appear to be different by haircolor

# ANOVA test using the python package "statsmodels"
# If this package is not installed in your machine, do "conda install statsmodels" in command prompt (Win) / terminal (Mac)
import statsmodels.api as sm
from statsmodels.formula.api import ols

mod = ols('painthreshold ~ haircolor', data=df).fit()
                
aov_table = sm.stats.anova_lm(mod)
print(aov_table)

             df       sum_sq     mean_sq         F    PR(>F)
haircolor   3.0  1360.726316  453.575439  6.791407  0.004114
Residual   15.0  1001.800000   66.786667       NaN       NaN

# post hoc testing

from statsmodels.stats.multicomp import pairwise_tukeyhsd
print(pairwise_tukeyhsd(df['painthreshold'], df['haircolor']))

        Multiple Comparison of Means - Tukey HSD, FWER=0.05         
====================================================================
    group1        group2     meandiff p-adj   lower    upper  reject
--------------------------------------------------------------------
   Dark Blond  Dark Brunette    -13.8 0.0742 -28.6977  1.0977  False
   Dark Blond    Light Blond      8.0 0.4369  -6.8977 22.8977  False
   Dark Blond Light Brunette     -8.7  0.416 -24.5014  7.1014  False
Dark Brunette    Light Blond     21.8 0.0037   6.9023 36.6977   True
Dark Brunette Light Brunette      5.1 0.7697 -10.7014 20.9014  False
  Light Blond Light Brunette    -16.7 0.0367 -32.5014 -0.8986   True
--------------------------------------------------------------------

Important: The tukeyhsd of statsmodels doesn't return P value. https://stackoverflow.com/questions/16049552/what-statistics-module-for-python-supports-one-way-anova-with-post-hoc-tests-tu

To view p-value, use pingouin python package.

#using pingouin package https://pingouin-stats.org/generated/pingouin.anova.html#pingouin.anova

aov = pg.anova(data=df, dv='painthreshold', between='haircolor', detailed=True)
aov

	Source	SS	DF	MS	F	p-unc	np2
0	haircolor	1360.726316	3	453.575439	6.791407	0.004114	0.575962
1	Within	1001.800000	15	66.786667	NaN	NaN	NaN

pg.pairwise_ttests(data=df, dv='painthreshold', between='haircolor')

	Contrast	A	B	Paired	Parametric	T	dof	Tail	p-unc	BF10	hedges
0	haircolor	Dark Blond	Dark Brunette	False	True	2.474565	8.000000	two-sided	0.038436	2.183	1.413596
1	haircolor	Dark Blond	Light Blond	False	True	-1.419100	8.000000	two-sided	0.193635	0.875	-0.810661
2	haircolor	Dark Blond	Light Brunette	False	True	1.752072	6.562510	two-sided	0.126065	1.133	0.982361
3	haircolor	Dark Brunette	Light Blond	False	True	-4.090697	8.000000	two-sided	0.003482	10.877	-2.336811
4	haircolor	Dark Brunette	Light Brunette	False	True	-1.105652	6.821772	two-sided	0.306339	0.723	-0.626769
5	haircolor	Light Blond	Light Brunette	False	True	3.563964	6.772089	two-sided	0.009690	5.498	2.015280

The following groups look difference in terms of pain threshold:

• Dark Brunette Light Blond
• Light Blond Light Brunette

df.boxplot('painthreshold', by='haircolor')

<AxesSubplot:title={'center':'painthreshold'}, xlabel='haircolor'>

Another Dataset

# read PlantGrowth.csv and perform ANOVA test
# this data contains three groups (ctrl, trt1, trt2)

data = pd.read_csv("data/PlantGrowth.csv")
data.head()

	weight	group
0	4.17	ctrl
1	5.58	ctrl
2	5.18	ctrl
3	6.11	ctrl
4	4.50	ctrl

data.groupby('group').size()

group
ctrl    10
trt1    10
trt2    10
dtype: int64

data.groupby('group').mean()

	weight
group
ctrl	5.032
trt1	4.661
trt2	5.526

#Create a boxplot
data.boxplot('weight', by='group')

<AxesSubplot:title={'center':'weight'}, xlabel='group'>

Normality test

pg.normality(data).round(3)

	W	pval	normal
weight	0.983	0.892	True

ANOVA

# test any differences in weight among three groups

ctrl = data[data['group'] == 'ctrl']['weight']
trt1 = data[data['group'] == 'trt1']['weight']
trt2 = data[data['group'] == 'trt2']['weight']

# compute one-way ANOVA P value   
from scipy import stats  
      
f_val, p_val = stats.f_oneway(ctrl, trt1, trt2)  
  
print("One-way ANOVA P =", p_val, "F value", f_val)

One-way ANOVA P = 0.0159099583256229 F value 4.846087862380136

Since p value is less than 0.05, we can claim with high confidence that the three groups' weights are statistically different.

# ANOVA test using the python package "statsmodels"
# If this package is not installed in your machine, do "conda install statsmodels" in command prompt (Win) / terminal (Mac)
import statsmodels.api as sm
from statsmodels.formula.api import ols

mod=ols('weight ~ group', data=data).fit()

aov_table=sm.stats.anova_lm(mod)
print(aov_table)

#low p value --> significant difference exists among the groups 

            df    sum_sq   mean_sq         F   PR(>F)
group      2.0   3.76634  1.883170  4.846088  0.01591
Residual  27.0  10.49209  0.388596       NaN      NaN

You can alos run Post Hoc Analysis

# post hoc analysis

from statsmodels.stats.multicomp import pairwise_tukeyhsd

print(pairwise_tukeyhsd(data['weight'], data['group']))

Multiple Comparison of Means - Tukey HSD, FWER=0.05
===================================================
group1 group2 meandiff p-adj   lower  upper  reject
---------------------------------------------------
  ctrl   trt1   -0.371 0.3921 -1.0621 0.3201  False
  ctrl   trt2    0.494  0.198 -0.1971 1.1851  False
  trt1   trt2    0.865  0.012  0.1739 1.5561   True
---------------------------------------------------

Treatment Group #1's weight is statistically different from Treatment Group #2

#Create a boxplot
data.boxplot('weight', by='group')

<AxesSubplot:title={'center':'weight'}, xlabel='group'>

Appendix: using pingouin

# install pingouin https://pingouin-stats.org/ !pip install pingouin --user

import pingouin as pg

# https://github.com/raphaelvallat/pingouin/blob/master/notebooks/01_ANOVA.ipynb

df.groupby('haircolor')['painthreshold'].agg(['mean', 'std', 'count', 'var']).round(2)

	mean	std	count	var
haircolor
Dark Blond	51.2	9.28	5	86.20
Dark Brunette	37.4	8.32	5	69.30
Light Blond	59.2	8.53	5	72.70
Light Brunette	42.5	5.45	4	29.67

T-Test & ANOVA

Test the normality of the data

display(pg.normality(df['painthreshold']))                                    

	W	pval	normal
painthreshold	0.971204	0.800256	True

pg.normality(df, group='haircolor', dv='painthreshold')

	W	pval	normal
Light Blond	0.991032	0.983182	True
Dark Blond	0.939790	0.664456	True
Light Brunette	0.930607	0.597973	True
Dark Brunette	0.883214	0.324129	True

T-test

# T-test

lb = df[df['haircolor'] == 'Light Blond']['painthreshold']
db = df[df['haircolor'] == 'Dark Blond']['painthreshold']

pg.ttest(lb, db, correction=False)

	T	dof	tail	p-val	CI95%	cohen-d	BF10	power
T-test	1.4191	8	two-sided	0.193635	[-5.0, 21.0]	0.897518	0.875	0.24032

We can't reject the null hypothesis

ANOVA

from pingouin import anova

aov = pg.anova(data=df, dv='painthreshold', between='haircolor', detailed=True)
aov

	Source	SS	DF	MS	F	p-unc	np2
0	haircolor	1360.726316	3	453.575439	6.791407	0.004114	0.575962
1	Within	1001.800000	15	66.786667	NaN	NaN	NaN

The detailed ANOVA summary table includes the following columns: SS : sums of squares DF : degrees of freedom MS : mean squares (= SS / DF) F : F-value (test statistic) p-unc : uncorrected p-values np2 : partial eta-square effect size * * In one-way ANOVA, partial eta-square is the same as eta-square and generalized eta-square. In the example above, there is a main effect of group (F(3, 15) = 6.79, p = .004)), so we can reject the null hypothesis that the groups have equal means.

Tukey post-hocs

Often, you will want to compute post-hoc tests to look at the pairwise differences between the groups. For one-way ANOVA with equal variances between groups, the optimal test is the pairwise_tukey post-hoc test.

As one can see from the post-hoc summary table below, the light blond group has a significantly higher pain threshold than the dark brunette (p=.0037) and light brunette (p=.0367) groups.

pg.pairwise_tukey(data=df, dv='painthreshold', between='haircolor')

	A	B	mean(A)	mean(B)	diff	se	T	p-tukey	hedges
0	Dark Blond	Dark Brunette	51.2	37.4	13.8	5.168623	2.669957	0.074168	1.525213
1	Dark Blond	Light Blond	51.2	59.2	-8.0	5.168623	-1.547801	0.436903	-0.884182
2	Dark Blond	Light Brunette	51.2	42.5	8.7	5.482153	1.586968	0.416008	0.946285
3	Dark Brunette	Light Blond	37.4	59.2	-21.8	5.168623	-4.217758	0.003713	-2.409395
4	Dark Brunette	Light Brunette	37.4	42.5	-5.1	5.482153	-0.930291	0.769703	-0.554719
5	Light Blond	Light Brunette	59.2	42.5	16.7	5.482153	3.046249	0.036653	1.816432

What if my groups have unequal variances? (Homogeneity of variances)

Traditional ANOVA can be quite unstable when the groups have unequal variances (see Liu 2015). Therefore, it is recommanded to use a Welch ANOVA instead, followed by Games-Howell post-hoc tests, which do not require the groups to have equal variances.

#Create a boxplot
df.boxplot('painthreshold', by='haircolor')

<AxesSubplot:title={'center':'painthreshold'}, xlabel='haircolor'>

db = df[df['haircolor'] == 'Dark Blond']['painthreshold']
dbr = df[df['haircolor'] == 'Dark Brunette']['painthreshold']
lb = df[df['haircolor'] == 'Light Blond']['painthreshold']
lbr = df[df['haircolor'] == 'Light Brunette']['painthreshold']

print(stats.levene(db, lbr))
print(stats.levene(db, dbr, lb, lbr))

LeveneResult(statistic=1.6035809906291834, pvalue=0.24590629443407336)
LeveneResult(statistic=0.39274322169059017, pvalue=0.7600161269687682)

Perform Levene test for equal variances.

The Levene test tests the null hypothesis that all input samples are from populations with equal variances.

https://docs.scipy.org/doc/scipy-0.14.0/reference/generated/scipy.stats.levene.html

The above test is not significant meaning there is homogeneity of variances and you can proceed t-testing.

If the test were to be significant, you can use a Welch's t-test (from more than three groups) or Man Whitney U test (for two groups).

Non-parametric t-test

# non-parametric t-test (Man Whitney U test)
# https://pingouin-stats.org/generated/pingouin.mwu.html
pg.mwu(lb, db).round(2)

	U-val	tail	p-val	RBC	CLES
MWU	18.0	two-sided	0.3	-0.44	0.72

from scipy.stats import mannwhitneyu  #using scipy package

mannwhitneyu(lb,db, alternative='two-sided')

MannwhitneyuResult(statistic=18.0, pvalue=0.2962698714842864)

High p value --> We can't reject the null hypothesis

Non-parametric ANOVA test

kruskal test

db = df[df['haircolor'] == 'Dark Blond']['painthreshold']
dbr = df[df['haircolor'] == 'Dark Brunette']['painthreshold']
lb = df[df['haircolor'] == 'Light Blond']['painthreshold']
lbr = df[df['haircolor'] == 'Light Brunette']['painthreshold']

from scipy.stats import kruskal
stat, p = kruskal(db, dbr, lb,  lbr)
print(stat, p)

10.588630377524138 0.014171563303136903

welch test

# non-parametric ANOVA test
pg.welch_anova(data=df, dv='painthreshold', between='haircolor')

	Source	ddof1	ddof2	F	p-unc	np2
0	haircolor	3	8.329841	5.890115	0.018813	0.575962

# non-parametric post hoc testing
pg.pairwise_gameshowell(data=df, dv='painthreshold', between='haircolor')

	A	B	mean(A)	mean(B)	diff	se	T	df	pval	hedges
0	Dark Blond	Dark Brunette	51.2	37.4	13.8	5.576737	2.474565	7.906609	0.140091	1.413596
1	Dark Blond	Light Blond	51.2	59.2	-8.0	5.637375	-1.419100	7.942669	0.521984	-0.810661
2	Dark Blond	Light Brunette	51.2	42.5	8.7	4.965548	1.752072	6.562510	0.372203	1.044734
3	Dark Brunette	Light Blond	37.4	59.2	-21.8	5.329165	-4.090697	7.995416	0.014775	-2.336811
4	Dark Brunette	Light Brunette	37.4	42.5	-5.1	4.612664	-1.105652	6.821772	0.684843	-0.659283
5	Light Blond	Light Brunette	59.2	42.5	16.7	4.685794	3.563964	6.772089	0.037775	2.125137

Paired t- test: Same subject

• testing differences between two variables (father's and son's heights) linked to same subjects (or individuals)

height = pd.read_csv("data/father_son_height.csv")
height.head()

	Father	Son
0	65.0	59.8
1	63.3	63.2
2	65.0	63.3
3	65.8	62.8
4	61.1	64.3

height.boxplot()

<AxesSubplot:>

normality test for the same subject t-test

https://pythonfordatascience.org/paired-samples-t-test-python/

height['difference'] = height['Father'] - height['Son']
height['difference'].plot(kind='hist')

<AxesSubplot:ylabel='Frequency'>

stats.probplot(height['difference'], plot= plt)

((array([-3.2191808 , -2.95561487, -2.80864001, ...,  2.80864001,
          2.95561487,  3.2191808 ]),
  array([-11.2,  -9.3,  -9.3, ...,   7.4,   7.9,   9. ])),
 (2.7817405711806855, -0.9974025974025972, 0.9990451109611047))

stats.shapiro(height['difference'])

ShapiroResult(statistic=0.9983996152877808, pvalue=0.4234532117843628)

conclusion: data is normally distributed. (high p-value 0.42 --> parametric data)

stats.ttest_rel(height['Father'], height['Son'])

Ttest_relResult(statistic=-11.78631938916475, pvalue=3.0273733779822012e-30)

Conclusion of paired t-test: Fathers and sons have different heights.

if the data was non-parametric ... consider a non-parametric test (e.g., Wilcoxon)

results = stats.wilcoxon(height['Father'], height['Son'])
print("The t-statistic is %.3f and the p-value is %.3f." % results)

The t-statistic is 169091.000 and the p-value is 0.000.

Same conclusion: Fathers and sons have different heights.

#Create a plot
#plt.figure(figsize=(16,8))
plt.plot(height['Father'], label = 'Father')
plt.plot(height['Son'], label = 'Son')
plt.legend(loc='best')

<matplotlib.legend.Legend at 0x284804b7760>

# using pingouin

pg.ttest(height['Father'], height['Son'], paired=True).round(2)

	T	dof	tail	p-val	CI95%	cohen-d	BF10	power
T-test	-11.79	1077	two-sided	0.0	[-1.16, -0.83]	0.36	6.846e+26	1.0

References

• http://cogmaster-stats.github.io/python-cogstats/basic_statistics.html
• http://www.marsja.se/four-ways-to-conduct-one-way-anovas-using-python/#anovapy
• http://www.randalolson.com/2012/08/06/statistical-analysis-made-easy-in-python/
• http://cleverowl.uk/2015/07/01/using-one-way-anova-and-tukeys-test-to-compare-data-sets/
• https://pingouin-stats.org/generated/pingouin.ttest.html
• https://pythonfordatascience.org/paired-samples-t-test-python/